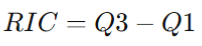Cuáles son las medidas de variabilidad o dispersión
Descubre las medidas clave de variabilidad en estadística: Varianza, Desviación Estándar, Desviación Media Absoluta, Rango y Rango Intercuartílico.
ESTADÍSTICA DESCRIPTIVAESTADISTICA
Camilo García Rey
11/29/20236 min read


Los estadísticos de variabilidad son medidas que se utilizan para comprender la dispersión o variación en un conjunto de datos.
Dentro de estos estimadores de variabilidad podemos encontrar aquellos que no requieren manejar los datos ordenados para ser analizados como lo son la varianza, la desviación estándar y desviación media absoluta, y por otro lado los que analizan la información a partir de datos ordenados como el rango y el rango intercuartílico.
Qué es la varianza
La varianza es una medida estadística que describe la dispersión o la extensión de un conjunto de datos. Es decir, indica cuánto se alejan los valores individuales de la media o promedio del conjunto de datos. Una varianza baja sugiere que los valores tienden a estar cercanos a la media, mientras que una varianza alta indica que los valores están más dispersos.
Cómo se calcula la varianza
La fórmula para calcular la varianza difiere ligeramente dependiendo de si estás trabajando con una población completa o solo con una muestra de esa población.
La fórmula para calcular la varianza para una población es la siguiente:
Donde:
N es el tamaño total de la población.
xi representa cada valor individual en la población
μ es la media de la población.
La fórmula para calcular la varianza para una muestra es la siguiente:
Donde:
n es el tamaño total de la población.
xi representa cada valor individual en la población
X̅ es la media de la población.
La diferencia entre las fórmulas de varianza de la población y la muestra radica en el denominador. Para una población, se utiliza N en el denominador, mientras que para una muestra se utiliza n−1. La razón detrás de esto es corregir el sesgo muestral y proporcionar una estimación no sesgada de la varianza de la población basada en la muestra.
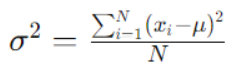
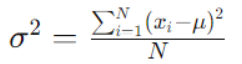
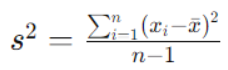
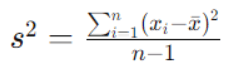
Qué es la desviación estándar
La desviación estándar o desviación típica es una medida estadística que cuantifica la cantidad de dispersión o variabilidad en un conjunto de datos. Es una de las medidas más utilizadas para describir la dispersión de los valores en un conjunto de datos. Una desviación estándar baja indica que los valores tienden a estar cerca de la media y de esa manera menos dispersos, mientras que una desviación típica alta indica que los valores están más alejados de la media y de esa manera más dispersos.
La fórmula para calcular la desviación estándar difiere ligeramente dependiendo de si estás trabajando con una población completa o solo con una muestra de esa población.
La fórmula para calcular la desviación estándar para una población es la siguiente:
Cómo se calcula la desviación estándar
Donde:
N es el tamaño total de la población.
xi representa cada valor individual en la población.
μ es la media de la población.
La fórmula para calcular la desviación estándar para una muestra es la siguiente:
Donde:
n es el tamaño de la muestra.
xi representa cada valor individual en la muestra.
X̅ es la media de la muestra.
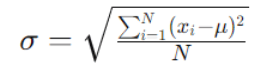
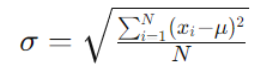
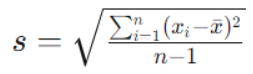
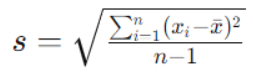
No, ni la varianza, ni la desviación estándar pueden ser negativas. Ambas medidas nunca podrán ser negativas debido a la forma en que se calculan.
La varianza se calcula tomando la media de las diferencias al cuadrado entre cada valor y la media del conjunto de datos. Dado que todas estas diferencias se elevan al cuadrado, los resultados son siempre no negativos. Por otro lado, la desviación estándar es simplemente la raíz cuadrada de la varianza. La raíz cuadrada de un número no negativo también es no negativa, por lo que la desviación estándar tampoco puede ser negativa.
La desviación estándar o la varianza pueden ser negativas?
Cuál es la diferencia entre la varianza y la desviación estándar
La desviación estándar es simplemente una versión más fácil de entender de la varianza, ya que elimina la elevación al cuadrado de los términos, colocando la medida de dispersión en la misma escala que los datos originales. La elección entre usar varianza o desviación estándar a menudo depende de la preferencia y la facilidad de interpretación.
Qué es la desviación media absoluta
La desviación media absoluta (DMA) o mean absolute deviation (MAD) en ingles es una medida de dispersión que calcula la magnitud promedio de las desviaciones individuales de los puntos de datos con respecto a la media aritmética.
La desviación media absoluta se calcula sumando las diferencias absolutas entre cada punto de datos y la media, y luego dividiendo este total por el número de observaciones. La DMA es útil para comprender la variabilidad en un conjunto de datos sin verse afectada por la dirección de las desviaciones, ofreciendo una perspectiva robusta de la dispersión.
Cuál es la fórmula de la desviación media absoluta
Donde:
n es el tamaño de la muestra.
xi representa cada valor individual en la muestra.
X̅ es la media de la muestra.
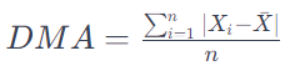
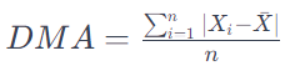
Qué es el rango
El rango es la diferencia entre el valor máximo y el valor mínimo en un conjunto de datos. Es una medida de dispersión que proporciona información sobre la variabilidad de los datos. Calcular el rango es útil para entender la amplitud o extensión de los valores observados en una muestra o población.
Como es una medida muy sensible a los datos atípicos, eventualmente y si el conjunto de datos y su contexto lo permite, para reducir esa sensibilidad se pueden eliminar los valores del límite superior e inferior de los datos.
Su formula simplemente implica restar el valor más bajo del valor más alto:
Qué es el rango intercuartílico
El rango intercuartílico (RIC) es la diferencia entre el tercer cuartil (Q3) y el primer cuartil (Q1), es decir la diferencia entre el percentil 25 y el 75 en un conjunto de datos. Este estadístico es robusto ante valores atípicos y proporciona una medida de la dispersión centrada en la media o mitad de los datos.
Calcular el (RIC) o (IQR) interquartile range en inglés es esencial para comprender la variabilidad de la parte central de la distribución, siendo una herramienta clave en análisis estadísticos y la detección de outliers.
Su formula consiste en restar al tercer cuartil, el primer cuartil de la distribución: