Cuáles son las medidas estadísticas de tendencia central

En el emocionante mundo de la estadística y la ciencia de datos relacionada con el marketing y los negocios, es esencial comprender una variedad de medidas y parámetros que son utilizados para resumir y desentrañar la información oculta en un conjunto de datos; son las llamadas medidas estadísticas de tendencia central o parámetros de localización estadística. Aquí exploraremos tres de estas medidas clave, explicaremos qué es la media, la mediana y la moda.

1. Cuáles son las medidas estadísticas de tendencia central

2. Que es tendencia central en estadística

3. Qué es la media

4. Cómo se calcula la media

5. Qué es la mediana

6. Cómo se calcula la mediana

7. Qué es la moda

8. Cómo se calcula la moda

9. Ejemplo de media, mediana y moda en Python

Además explicaremos estos conceptos mediante el ejemplo de una empresa que está analizando su CTR (Click-Through Rate) o tasa (%) de clics diarios de un anuncio, una métrica muy utilizada en RRSS. Este se calcula dividiendo el número de clics en un enlace o anuncio entre el número de impresiones o apariciones y multiplicando el resultado por 100.

Supongamos que fue publicado un anuncio en alguna red social durante un mes excluyendo los fines de semana, es decir que la campaña estuvo activa 21 días del mes. Y el primer lunes hubo 10.000 clics de 200.000 impresiones ese día. 

CTR = (10.000 clics / 200.000 impresiones) * 100 = 5%

Ya conociendo la formula de CTR se procederemos a analizará el rendimiento del anuncio al cabo de este periodo mediante el uso de las medidas de tendencia central.

La tendencia central en estadística se refiere al valor o valores que representan la ubicación central de un conjunto de datos. En otras palabras, son medidas que indican dónde se encuentra el "centro" de los datos y nos ayudan a responder preguntas como: ¿dónde se encuentra el valor medio en un conjunto de datos?" o ¿cuál es el valor más común?

Qué es tendencia central en estadística

La media en estadística, también conocida como promedio o media aritmética, es una medida de tendencia central que se calcula sumando todos los valores en un conjunto de datos y dividiéndolos por la cantidad de valores. Es una forma común de resumir datos y encontrar un valor central que represente el conjunto en su totalidad. La media puede ser sensible a valores extremos o valores atípicos en el conjunto de datos.

Qué es la media

Donde:

• Media (x̄): Representa el valor promedio o la media aritmética.

• Σ (sigma mayúscula): Indica la suma de los valores.

• xi: Cada valor individual en el conjunto de datos.

• N: Número total de valores en el conjunto de datos.

Por ejemplo, se calcula la media de los clics through rate (CTR) diarios para obtener un promedio de rendimiento durante el mes. Si nuestros CTR diarios por 21 días fueron: [1.0, 2.0, 0.5, 3.0, 2.0, 2.5, 3.5, 5.0, 4.0, 3.5, 2.6, 1.8, 1.1, 1.5, 1.0, 3.0, 3.5, 4.0, 5.0, 6.0, 7.0]

De esa manera la media seria:

Media = (Suma de todos los CTR) / (Número de días) =  (63.5) / (21) = 3.02 CTR promedio

Cómo se calcula la media

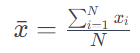
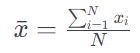
Para obtener la media se suman todos los valores que tenemos en el conjunto de datos y los dividimos por le número de datos que conforman el dataset.

La mediana en estadística es otra medida de tendencia central que se encuentra ordenando todos los valores según su tamaño y eligiendo el valor que se encuentra en el centro de la lista de datos. En otras palabras, es el valor que divide el conjunto de datos en dos mitades iguales cuando los valores se organizan en orden. La mediana es menos sensible a los valores atípicos en comparación con la media, por lo que a menudo se utiliza cuando se sospecha que puede haber valores atípicos en los datos.

Qué es la mediana

Cómo se calcula la mediana

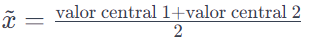
Tomando un nuevo conjunto par de diez datos, tomamos los dos valores centrales, los sumamos y los dividimos en 2.

Clics ordenados: [2.0, 2.5, 2.6, 3.0, 3.5, 4.0, 4.5, 4.6, 5.0, 6.0] 

Mediana = 3.5 + 4.0 / 2 = 3.75

Si tienen un número impar de valores en tu conjunto de datos podrás fácilmente identificar el valor de la mitad y allí tendrías la media.

Basándonos en el mismo ejemplo de arriba, ordenamos nuestro conjunto de datos de menor a mayor y tomamos el numero que se encuentra en el medio, es decir quedan diez valores a la izquierda de la mediana y otros diez valores a la derecha de la mediana 3.0.

CTR ordenados: [0.5, 1.0, 1.0, 1.1, 1.5, 1.8, 2.0, 2.0, 2.5, 2.6, 3.0, 3.0, 3.5, 3.5, 3.5, 4.0, 4.0, 5.0, 5.0, 6.0, 7.0]

Sin embargo, si tienes un conjunto de datos par puedes aplicar la siguiente formula para obtener la mediana.

La moda en estadística se refiere al valor o valores que aparecen con mayor frecuencia en un conjunto de datos. En otras palabras, es el valor o los valores que ocurren con la mayor frecuencia en un conjunto de observaciones. La moda es una medida de tendencia central y es especialmente útil cuando se trabaja con datos categóricos o discretos, como categorías de productos, colores o calificaciones.

Qué es la moda

Si dentro de nuestro conjunto de datos tenemos un valor que aparece con mayor frecuencia que cualquier otro tendremos una moda unimodal, si tenemos dos valores iguales y con las mayores frecuencias, tendremos una moda bimodal y cuando tenemos más de dos modas se dice que es una moda multimodal. Si el dataset contiene más de una moda, los datos te están diciendo que tendrías múltiples tendencias o picos en su distribución, y es muy posible que luego detectar ese fenómeno mediante la visualización debas realizar un análisis de segmentado, es decir separar el conjunto principal en subconjunto y hacer su análisis por separado.  

Teniendo en cuenta el mismo ejemplo anterior acá encontraremos una moda unimodal, dado que encontramos solo 1 moda, en este caso 3.5 se repiten 3 veces.

CTR ordenados: [0.5, 1.0, 1.0, 1.1, 1.5, 1.8, 2.0, 2.0, 2.5, 2.6, 3.0, 3.0, 3.5, 3.5, 3.5, 4.0, 4.0, 5.0, 5.0, 6.0, 7.0] entonces la Mediana = 3.5

Cómo se calcula la moda

A continuación, haremos el análisis del caso a través del uso de Python y su librería statistics, haciendo uso de las medidas de tendencia central mencionadas.

Ejemplo de media, moda y mediana en Python

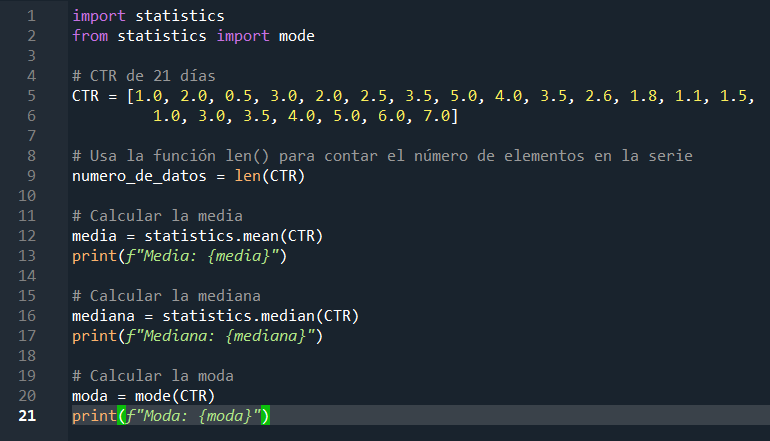
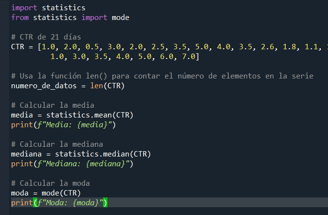
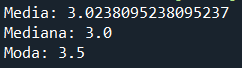
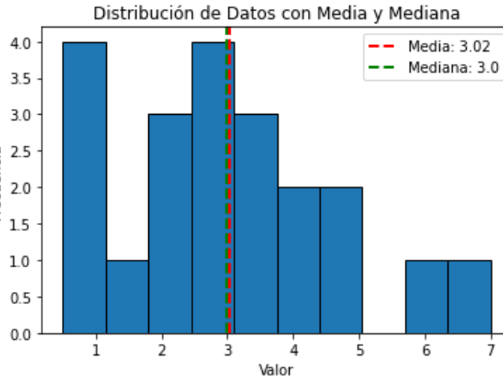
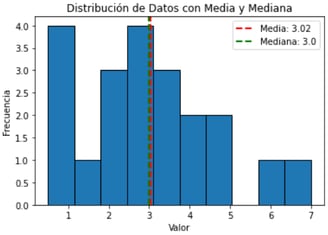
A continuación, haremos el análisis del caso a través del uso de Python y su librería statistics, haciendo uso de las medidas de tendencia central mencionadas. Recordemos que la media es la suma de todos los valores dividida por la cantidad de valores. En este caso, la media 3.02 aproximadamente. Esto nos dice que los valores de la serie de datos tienden a estar alrededor de 3. La mediana que es el valor del medio es 3.0. Esto indica que el 50% de los datos son menores o iguales a 3.0, y el 50% son mayores o iguales a 3.0. Mientras que la moda es 3.5, este es el valor más frecuente. Esto significa que 3.5 es el valor que más se repite en la serie.

En conclusión, la tendencia central de los datos es relativamente cercana, como podemos ver los resultados de la media y la mediana, lo que indica que la distribución de los datos tiende a estar centrada alrededor de estos valores, y tienden a agruparse alrededor de 3, a pesar de que exista un pico hacia el 1. Además, como la media y la mediana están muy cerca podríamos inferir que la distribución es casi simétrica dado que la presencia de una moda en 3.5 indica que hay un pico en la distribución en ese punto, lo que podría sugerir una ligera asimetría hacia la derecha.