Explorando la distribución de los datos univariados mediante gráficos

Cuando vamos a explorar la distribución de datos univariados, las herramientas mas utilizadas son la tabla de frecuencia que actúa como nuestra brújula inicial, proporcionando una visión rápida de la frecuencia de cada valor en nuestros datos, seguido por el histograma y el gráfico de densidad, revelando la forma y estructura de la distribución de datos de forma simple pero muy informativa y finalmente con el boxplot, ofreciendo una visión compacta pero informativa de la variabilidad de los datos, destacando posibles outliers y resumiendo la dispersión en un solo vistazo.

En esta entrada definiremos cada uno de los gráficos mencionados y explicaremos mediante el ejemplo de una empresa que realizo una campaña de marketing online durante un mes orientada al los usuarios de la parte inferior del embudo del nivel de conversión de funnel o embudo de marketing y obtuvo las siguientes tasas de conversión diarias por 30 días, estas tasas son porcentuales:

tasa_conversion= [3.2, 4.5, 2.8, 3.2, 4.5, 3.7, 2.5, 3.8, 4.5, 2.5, 4.1, 3.4, 2.9, 3.2, 4.4, 4.4, 2.7, 3.3, 4.6, 3.3, 4.8, 2.9 ,4.1 ,5.4 ,4.1 ,4.6 ,2.8 ,2.7 ,2.9 ,7.0]

Recordemos que la tasa de conversión se da en porcentaje se utiliza para medir el porcentaje de visitantes que realizan una acción deseada es decir una conversión, ya sea hacer una compra, llenar un formulario o suscribirse a un servicio. Esta fórmula te dará el porcentaje de visitantes que han realizado la acción deseada en comparación con el total de visitantes.

1. Explorando la distribución de los datos univariados mediante gráficos

2. Qué es una tabla de frecuencia

3. Ejemplo de tabla de frecuencia en Python

4. Qué es un histograma

5. Ejemplo de histograma en Python

6. Qué es un gráfico de densidad

7. Ejemplo de gráfico de densidad en Python

8. Qué es un boxplot

9. Ejemplo de boxplot en Python
   

Qué es una tabla de frecuencia

Una tabla de frecuencia, una representación tabular esencial en estadísticas descriptivas, ofrece una visión organizada y resumida de la distribución de frecuencias de diversos valores en un conjunto de datos. Esta herramienta proporciona información valiosa al indicar con qué frecuencia cada valor específico aparece en los datos, brindando claridad y concisión en la presentación de la información. Se puede utilizar para datos cualitativos como cuantitativos.

Entre los elementos clave que suelen incluirse en una tabla de frecuencia se encuentran la frecuencia, que destaca cuántas veces se repite cada valor en el conjunto de datos; la frecuencia relativa, que expresa la proporción de veces que aparece cada valor en relación con el total de observaciones; y la frecuencia acumulada, que representa la suma acumulativa de las frecuencias hasta el valor actual, culminando en un total coherente con el tamaño total del conjunto de datos. Esta herramienta, al revelar patrones y tendencias, se convierte en un recurso invaluable para identificar características significativas en los datos y comprender la estructura subyacente del conjunto de información.

Ejemplo de tabla de frecuencia en Python

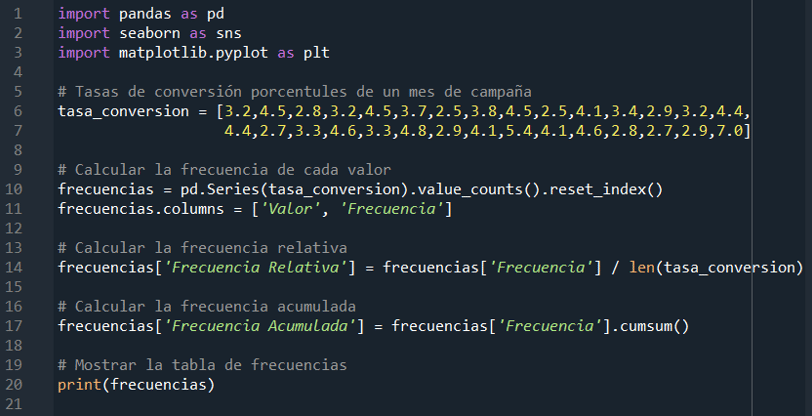
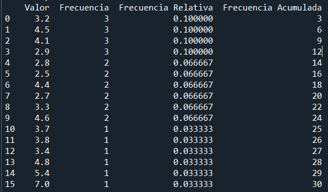
En el código, se llevó a cabo un análisis detallado de las tasas de conversión de un mes de campaña. Después de importar las bibliotecas necesarias, se definieron los datos en la lista tasa_conversion. Luego, mediante pandas, se calcularon las frecuencias de cada valor y se organizó la información en un DataFrame. Posteriormente, se determinaron las frecuencias relativas dividiendo cada frecuencia por la longitud total de los datos. Asimismo, se calculó la frecuencia acumulada sumando secuencialmente las frecuencias. Finalmente, la tabla de frecuencias resultante se imprimió en la consola, proporcionando una visión completa de la distribución y variabilidad de las tasas de conversión, lo que facilita una comprensión más profunda de los patrones en los datos.

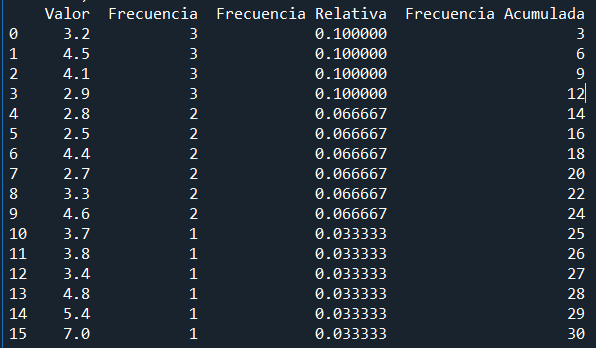
Al ver la tabla de frecuencia podemos observar una variabilidad significativa. Valores como 3.2, 4.1, 4.5 y 2.9 lideran en frecuencia, indicando un centro de la distribución, aunque la mediana no está claramente definida en la tabla. La presencia de valores extremos, como 7.0 y 5.4, sugiere posibles outliers. Las frecuencias relativas proporcionan una perspectiva proporcional de cada valor, mientras que la frecuencia acumulada muestra cómo se acumulan las ocurrencias. Sin embargo para una comprensión más completa de la forma de la distribución, se recomienda la visualización mediante un histograma.

Un histograma es una representación gráfica efectiva para visualizar la distribución de frecuencias de un conjunto de datos. Este gráfico divide el rango de valores en intervalos, conocidos como "bins", y muestra cuántas observaciones caen dentro de cada intervalo. Cada barra en el histograma representa un intervalo de valores, y la altura de la barra indica la frecuencia o el número de observaciones en ese intervalo. Esta herramienta es valiosa para identificar patrones en la concentración de datos, como la presencia de modas (picos) o sesgos en la distribución, y es ideal para representar datos continuos.

Los elementos clave de un histograma incluyen el eje X (horizontal), que representa la variable continua y se divide en intervalos, y el eje Y (vertical), que muestra la frecuencia o densidad de ocurrencias en cada intervalo. Las barras verticales y continuas se dibujan sobre cada intervalo en el eje X, con su altura proporcional a la frecuencia o densidad en ese intervalo. La versatilidad del histograma radica en su capacidad para manejar datos con diferentes características, y su análisis proporciona información sobre la tendencia central, dispersión y cualquier agrupamiento de datos. En el ámbito del análisis exploratorio de datos, el histograma es una herramienta fundamental para comprender la forma y la estructura de los conjuntos de datos.

Qué es un histograma

Ejemplo de histograma en Python

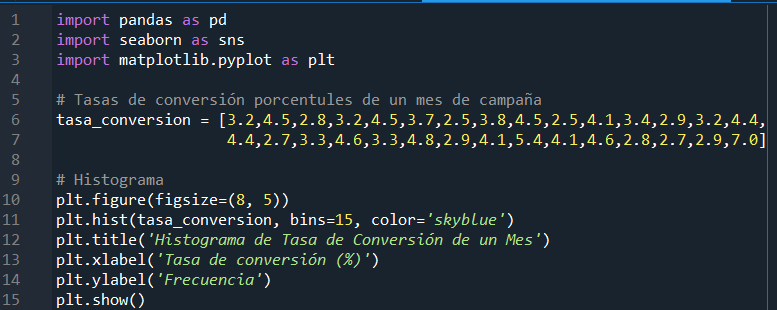
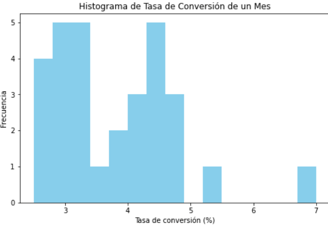
El código comienza importando las bibliotecas necesarias, como pandas, seaborn y matplotlib.pyplot. Luego, se define la variable "tasa_conversion" que contiene las tasas de conversión mensuales. La figura del histograma se configura con un tamaño específico, y utilizando plt.hist, se crea el histograma que representa la distribución de estas tasas de conversión. Se especifica el numero de bins o baras en 15 así como el color del histograma "skyblue", y se añaden etiquetas a los ejes para mayor claridad. Finalmente, con plt.show(), se visualiza el histograma. Este enfoque proporciona una representación gráfica efectiva de la distribución de las tasas de conversión, permitiendo la identificación visual de tendencias y patrones en los datos.

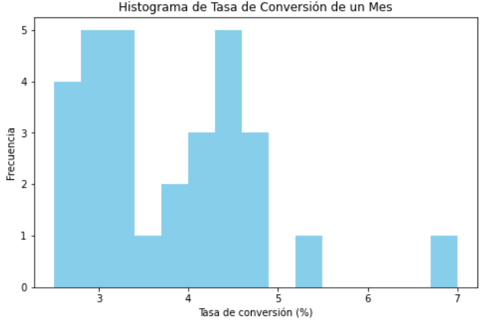
El código proporciona una representación visual de la distribución de las tasas de conversión mensuales mediante un histograma. La forma asimétrica de la distribución sugiere una concentración mayor en tasas de conversión más bajas, con notables frecuencias alrededor de 3.2, 4.5, 2.9 y 4.1. La presencia de valores más altos, como 7.0 y 5.4, indica cierta variabilidad en los datos. Este enfoque visual facilita la identificación de patrones y ofrece insights sobre la distribución y tendencias en las tasas de conversión.

Qué es un gráfico de densidad

Un gráfico de densidad es una herramienta visual que ofrece una representación suave y continua de la distribución de datos de un conjunto de datos de tipo continuo. El gráfico de densidad utiliza curvas suaves para visualizar la función de densidad de probabilidad (PDF). Esta función proporciona una estimación de cómo se distribuyen los datos a lo largo del rango continuo, destacando la forma y la concentración de la distribución. Además, el área bajo la curva en un gráfico de densidad totaliza 1, lo que implica que el área bajo la curva dentro de un intervalo específico refleja la probabilidad de que una observación caiga en ese rango.

Las características distintivas de los gráficos de densidad los hacen particularmente útiles para la comparación visual de diferentes conjuntos de datos. Al superponer múltiples curvas de densidad en el mismo gráfico, es posible analizar de manera efectiva las diferencias en la distribución entre los conjuntos de datos, permitiendo una comprensión detallada de las variaciones y similitudes en sus características probabilísticas.

Ejemplo de gráfico de densidad en Python

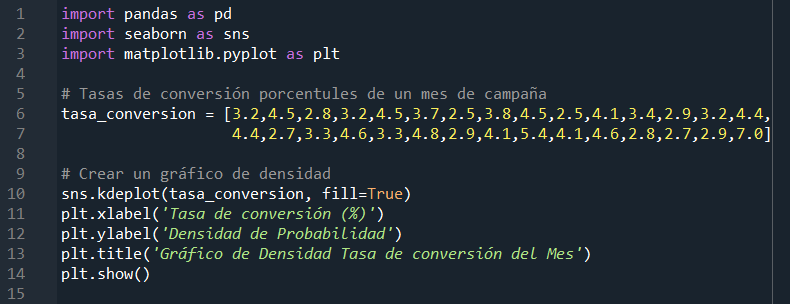
Este código utiliza las bibliotecas pandas, seaborn y matplotlib.pyplot para crear y visualizar un gráfico de densidad de las tasas de conversión mensuales. Primero, se define la lista "tasa_conversion" que contiene las tasas de conversión del mes de la campaña. Luego, se utiliza la función sns.kdeplot() para crear el gráfico de densidad, que representa la distribución de las tasas de conversión en forma de una curva suavizada. El parámetro fill=True agrega color al área bajo la curva para resaltar la densidad de probabilidad. Después, se añaden etiquetas a los ejes x e y, así como un título al gráfico. Finalmente, con plt.show(), se visualiza el gráfico de densidad, proporcionando una representación visual de la distribución de las tasas de conversión y destacando áreas de concentración y variabilidad en los datos.

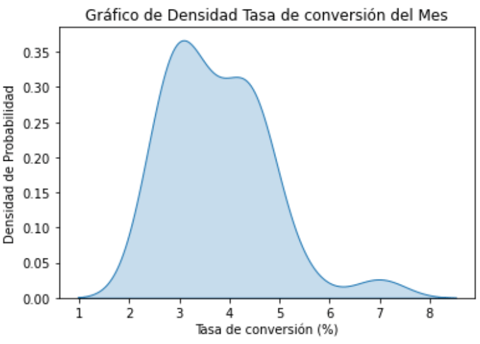
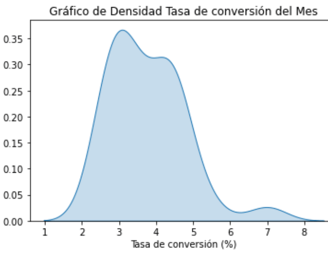
El gráfico de densidad generado revela una distribución suavizada de las tasas de conversión mensuales. La forma sesgada hacia la derecha o que cola derecha de la curva es más larga sugiere que la mayoría de las tasas de conversión se encuentran en el rango medio, alrededor de 3.0 a 4.0. La densidad de probabilidad, representada por el área bajo la curva, destaca un pico en esta región, indicando una concentración significativa de datos. Sin embargo, las colas extendiéndose hacia valores más altos señalan la presencia de tasas de conversión más elevadas, aunque menos frecuentes.

Qué es un boxplot

El boxplot, también denominado diagrama de caja y bigotes, es una representación gráfica que ofrece información detallada acerca de la distribución y variabilidad de un conjunto de datos. Este gráfico consta de una caja y dos "bigotes" que se extienden desde sus extremos. La caja abarca el rango intercuartílico (IQR), que representa la distancia entre el primer cuartil (Q1) y el tercer cuartil (Q3), cubriendo así el 50% central de los datos. Los bigotes, líneas que se prolongan desde la caja, indican la extensión de los valores dentro de un rango específico, relacionándose con la dispersión de los datos. Dentro de la caja, se traza una línea que representa la mediana del conjunto de datos, mientras que puntos individuales fuera de los bigotes, conocidos como valores atípicos u outliers, pueden señalar valores extremadamente altos o bajos.

Esta herramienta visual es eficaz para identificar la simetría de la distribución, evaluar la dispersión de los datos y detectar la presencia de valores atípicos. Ampliamente utilizado en estadísticas descriptivas y análisis exploratorio de datos continuos, el boxplot proporciona una visión rápida y precisa de las características clave de un conjunto de datos.

Ejemplo de boxplot en Python

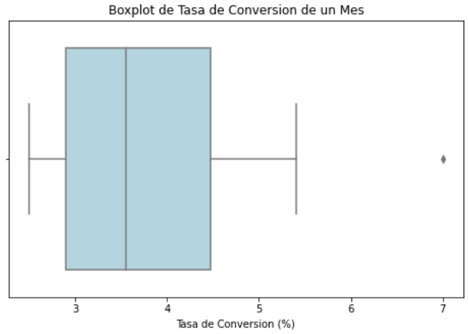
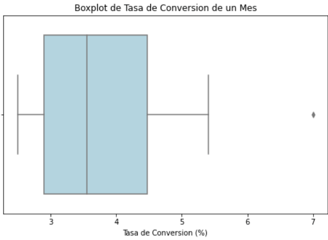
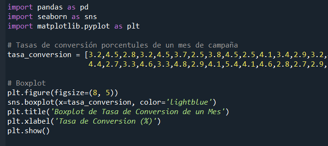
Este código utiliza las bibliotecas pandas, seaborn y matplotlib.pyplot para realizar un análisis visual de la distribución de las tasas de conversión mensuales mediante un boxplot. En primer lugar, se define la lista tasa_conversion que contiene las tasas de conversión del mes de la campaña. Luego, se configura el tamaño de la figura y se crea el boxplot utilizando sns.boxplot(), donde el eje x representa las tasas de conversión y se utiliza un color 'lightblue' para mejorar la legibilidad. Finalmente, se añaden títulos y etiquetas a los ejes para proporcionar una interpretación clara del gráfico. Este enfoque visual permite identificar patrones, tendencias y la presencia de valores atípicos en la distribución de las tasas de conversión, brindando una representación efectiva de la variabilidad de los datos.

El boxplot generado a partir del conjunto de tasas de conversión mensuales revela varios aspectos importantes de la distribución. La mediana se sitúa alrededor de 3.5, indicando que aproximadamente la mitad de las tasas de conversión están por encima y por debajo de este valor. La variabilidad intercuartílica, representada por la longitud de la caja, parece ser moderada, abarcando desde aproximadamente 2.8 hasta 4.4. Además, la presencia de un valor atípico en torno a 7.0 se destaca visualmente, sugiriendo una asimetría hacia tasas de conversión más altas. A pesar de esta asimetría, la concentración general de datos alrededor de la mediana indica que la mayoría de las tasas de conversión se encuentran en un rango relativamente estrecho. En conjunto, este boxplot proporciona una representación visual clara de la distribución, centralidad y variabilidad de las tasas de conversión, identificando patrones clave y valores atípicos en el conjunto de datos.