Qué es un valor atípico en estadística

En el ámbito de la estadística, se denomina valor atípico u outlier a aquel valor que se aparta significativamente del conjunto general de datos. La presencia de valores atípicos puede atribuirse a diversos factores, tales como errores de medición, eventos excepcionales o simplemente la variabilidad inherente a los datos. Es crucial destacar que estos valores atípicos tienen el potencial de impactar negativamente en el análisis de datos y en las medidas de tendencia central, como la media, ya que pueden distorsionar la interpretación de los resultados. Por consiguiente, resulta fundamental identificar y, en determinadas circunstancias, abordar los valores atípicos antes de llevar a cabo cualquier análisis estadístico. en algunos casos, tratar los valores atípicos antes de realizar algún análisis estadístico.

1. Qué es un valor atípico en estadística

2. Como identificar un valor atípico

3. Ejemplo de detección de outliers

Como identificar un valor atípico

Algunos de los métodos más sencillos para identificar los outlier son los siguientes:

1. Diagrama de Caja o Boxplot

Este gráfico visualiza la distribución de los datos, destacando cualquier valor que se encuentre fuera de los llamados "bigotes" del diagrama. Los puntos más allá de estos límites suelen considerarse como posibles valores atípicos.

2. Usar el Criterio del Rango Intercuartílico (IQR)

Se calcula el rango intercuartílico, que es la diferencia entre el tercer cuartil (Q3) y el primer cuartil (Q1). Los valores que caen fuera de este rango (por debajo de Q1 - 1.5 IQR o por encima de Q3 + 1.5 IQR) se consideran atípicos.

3. Z-Score

Se calcula la puntuación Z para cada observación, midiendo cuántas desviaciones estándar se encuentra un valor con respecto a la media del conjunto de datos. Los valores con un Z-Score significativamente alto o bajo pueden indicar la presencia de valores atípicos.

4. Métodos basados en la Distribución

Algunos métodos asumen una distribución específica de los datos y identifican como atípicos aquellos valores que se desvían considerablemente de dicha distribución mediante pruebas estadísticas.

5. Visualización Gráfica Adicional

Utilizar gráficos adicionales, como gráficos de dispersión o gráficos de probabilidad normal, puede ayudar a detectar patrones inusuales que podrían indicar la presencia de valores atípicos.

6. Uso de Algoritmos:

Algoritmos específicos, como el método de clustering, pueden identificar valores atípicos en conjuntos de datos más complejos.

7. Conocer el contexto del problema:

Comprender el contexto del dominio de los datos es crucial. Algunos valores que podrían parecer atípicos pueden tener sentido en un contexto específico.

alcance = [ 3381, 2973, 2242, 122, 2674, 3435, 2065, 5007, 1550, 1416, 2724, 3327, 1220, 3424, 2810, 542, 5166, 3420, 1041, 3973, 10738, 325, 10024, 3232, 8580, 7206 ]

Ejemplo de detección de outliers

A continuación, revisaremos el concepto de valores atípicos a través del ejemplo de una empresa que desea analizar el alcance de sus publicaciones en Instagram de sus seguidores actuales durante un mes. Recordemos que el alcance de una publicación en RRSS es el número de usuarios únicos que ven una publicación, es decir si esa publicación es vista 2 o 3 veces por el mismo seguir, solo se tendría en cuenta una sola vez en la métrica de alcance orgánico.

Supongamos que el community manager realizo un post semanal en el feed del instagram de su empresa durante el primer semestre es decir 26 semanas, que contó con un promedio de 20.000 seguidores semestrales y el equipo de marketing desea revisar si hubo algunos posts que tuvieron un alcance extraordinario. Estos fueron los alcances de cada publicación semanal:

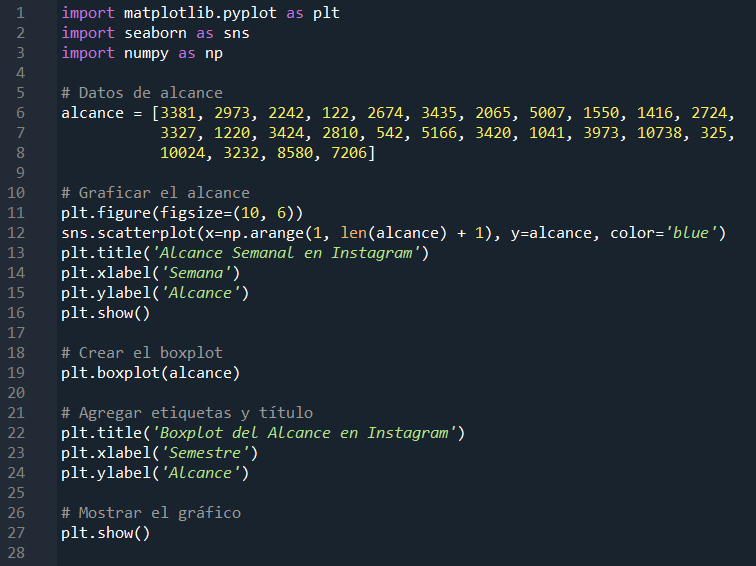
En el código anterior podemos observar la descarga de las librerías que nos permitirán realizar un scatterplot o diagrama de dispersión y un boxplot o diagrama de caja o bigotes. El primero nos puede ayudar a visualizar la relación entre las 2 variables en cuestión, alcance vs semana y además observar si hay valores atípicos. Mientras que el boxplot nos ayuda a resumir la distribución de los datos mediante la visualización de cuartiles, además de ver más claramente los outliers, dado que en un boxplot, la distancia entre el primer cuartil (Q1) y el tercer cuartil (Q3) se conoce como el Rango Intercuartílico (IQR, por sus siglas en inglés). La fórmula para calcular el IQR es:

IQR = Q3 − Q1

Y la regla general para identificar valores atípicos en un boxplot es utilizar los "bigotes" del gráfico. Los bigotes suelen extenderse hasta 1.5 veces el IQR por encima de Q3 y por debajo de Q1. Cualquier punto fuera de estos límites se considera un valor atípico.

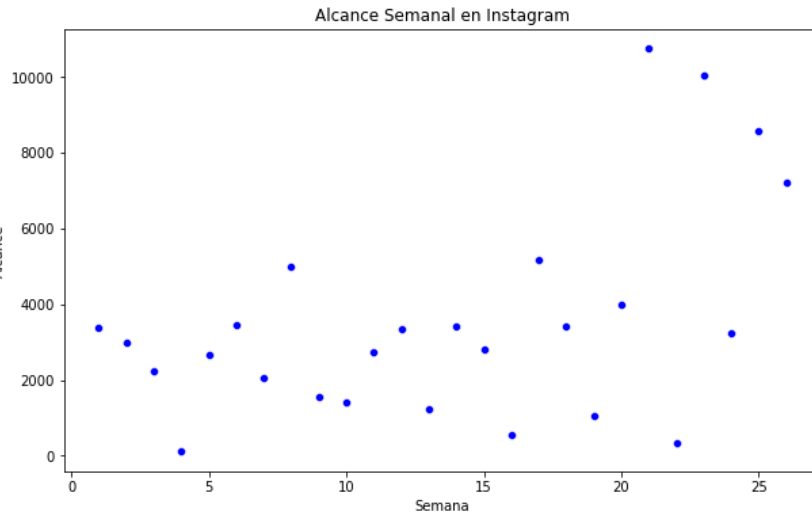
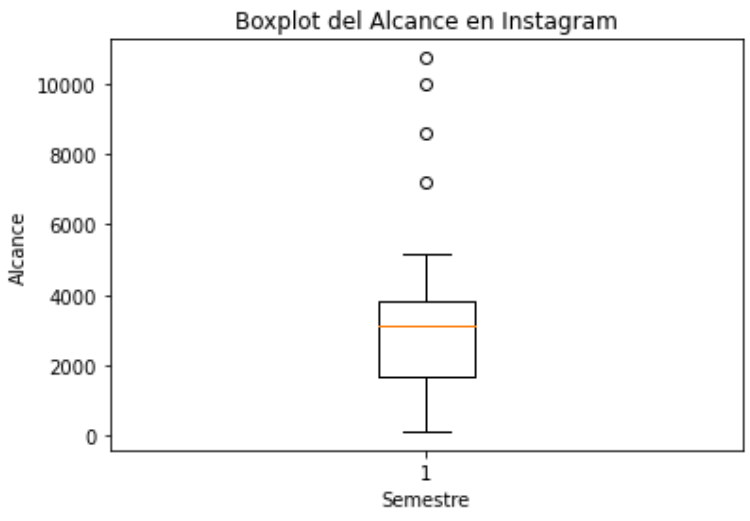
En el scatterplot podemos identificar 4 puntos al costado superior derecho de la imagen que tienen una posición que difiere significativamente de los demás. Y a través del boxplot como lo vemos en la segunda imagen podemos verificar que tenemos 4 puntos a una distancia que se extiende hasta 1.5 veces el IQR por encima de Q3, como lo vemos en la parte superior del grafico.

De esta manera podemos concluir que sí hay publicaciones que han tenido un alcance significativamente diferente al resto, en este caso mayor al resto. Además podemos ver que hay una mayor dispersión de los datos inferiores a la mediana y una menor dispersión de los valor superiores a la mediana, sin contar con los outliers.