Qué son las series de tiempos o series temporales

Las series de tiempo son secuencias ordenadas cronológicamente de valores, donde cada punto de datos representa una observación de una variable en un momento específico. Estas variables pueden ser continuas, como la temperatura o el precio de una acción, o discretas, como el número de clientes o defectos en un producto.

1. Qué son las series de tiempos

2. Cuáles son las características de las series de tiempos

3. Cuáles son los componentes de las Series de Tiempo

4. Cuáles son los objetivos de un análisis de series de tiempo

5. Pasos para realizar un análisis de las series temporales

Cuáles son las características de las series de tiempos

Equiespaciado e Intervalos Irregulares: Las observaciones en una serie de tiempo suelen registrarse a intervalos regulares de tiempo, como diario, mensual o anual. No obstante, también existen series de tiempo con intervalos de tiempo irregulares, donde las observaciones pueden estar espaciadas de manera no uniforme.

Dependencia Temporal: En una serie de tiempo, las observaciones están típicamente correlacionadas entre sí. Esto implica que el valor de una observación en un momento dado puede ser influenciado por los valores de observaciones anteriores, reflejando así una dependencia temporal en los datos.

Cuáles son los componentes de las Series de Tiempo

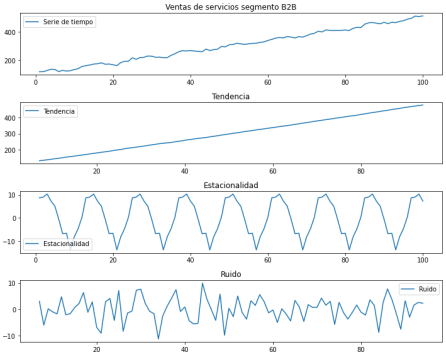
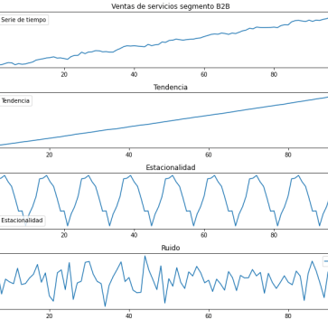
Las series de tiempo pueden descomponerse en 4 componentes:

Nivel: Representa la tendencia general de la serie, mostrando la dirección predominante en la que los datos evolucionan a largo plazo.

Tendencia: Indica la dirección y la tasa de cambio del nivel a lo largo del tiempo, permitiendo identificar patrones de crecimiento, declive o estabilidad en la serie.

Estacionalidad: Refleja fluctuaciones regulares en la serie que se repiten a lo largo de intervalos de tiempo fijos, como estacionalidad anual o mensual.

Ruido: Representa las variaciones aleatorias o irregulares en la serie que no pueden ser explicadas por los otros componentes. Este ruido es impredecible y refleja la incertidumbre inherente en los datos.

Cuáles son los objetivos de un análisis de series de tiempo

Un análisis de series de tiempo se realiza con diferentes fines,, entre ellos tenemos:

Descripción: Comprender las características básicas de una serie de tiempo, como su nivel, tendencia, estacionalidad y ruido.

Pronóstico: Predecir el valor futuro de una variable en una serie de tiempo.

Explicación: Identificar los factores que causan los patrones observados en una serie de tiempo.

Control: Desarrollar estrategias para influir en el comportamiento futuro de una serie de tiempo.

Pasos para realizar un análisis de series temporales

El orden ideal para realizar un análisis de una serie de tiempo depende de las características específicas de la serie y de los objetivos del análisis. Sin embargo, en general, se recomienda seguir un orden secuencial que permita aprovechar la información obtenida en cada etapa para guiar las etapas posteriores.

A continuación, se presenta un orden recomendado para el análisis de series de tiempo:

1. Visualización de datos: Comience por visualizar la serie de tiempo utilizando gráficos como el gráfico de líneas, el gráfico de barras o el diagrama de dispersión. La visualización de datos le permitirá observar patrones generales, tendencias, estacionalidad y posibles anomalías en la serie.

Adicionalmente y de acuerdo al caso podría También, podría optar por gráficos de auto correlación: Estos gráficos muestran la correlación entre las observaciones en una serie de tiempo y las observaciones en momentos anteriores. O gráficos de correlación cruzada para visualizar la correlación relación entre dos series de tiempo.

2. Exploración descriptiva: Calcule medidas descriptivas como la media, la mediana, la moda, la desviación estándar, el rango, etc. Estas medidas le proporcionarán información básica sobre la distribución de los valores en la serie.

3. Análisis de estacionariedad: Determine si la serie de tiempo es estacionaria o no estacionaria. La estacionariedad implica que las propiedades estadísticas de la serie, como la media y la varianza, permanecen constantes a lo largo del tiempo. Esto nos permite suponer que las relaciones observadas en el pasado se mantendrán en el futuro.

Existen pruebas estadísticas para evaluar la estacionariedad, como la prueba de Dickey-Fuller (ADF) y la prueba KPSS, las cuales son complementarias, y la de Phillips-Perron (PP) entre otras.

4. Descomposición de la serie: Si la serie de tiempo es no estacionaria, descompóngala en sus componentes de nivel, tendencia y estacionalidad. La descomposición permite aislar cada componente y analizarlo por separado.

Existen diferentes métodos de descomposición, como el método aditivo, el método multiplicativo y el método de Holt-Winters.

5. Suavizado de la serie: Si la serie de tiempo tiene ruido significativo, suavícela utilizando técnicas como los promedios móviles, la suavización exponencial o el filtrado de Kalman. El suavizado permite eliminar el ruido y resaltar las tendencias subyacentes de la serie.

6. Selección del modelo estadístico: En base a la información obtenida en las etapas anteriores, seleccione un modelo estadístico adecuado para la serie de tiempo. La elección del modelo dependerá de las características de la serie, como la estacionariedad, la presencia de estacionalidad, la estructura de autocorrelación, etc.

Algunos modelos estadísticos comunes para series de tiempo incluyen modelos ARIMA, modelos de regresión con autocorrelación, modelos de series de tiempo con heterocedasticidad y modelos de series de tiempo no lineales.

7. Ajuste del modelo y evaluación: Ajuste el modelo estadístico seleccionado a los datos de la serie de tiempo. Evalúe el rendimiento del modelo utilizando métricas como el error cuadrático medio (MSE), el error cuadrático medio raíz (RMSE) o el criterio de Akaike (AIC).

8. Interpretación y predicción: Interprete los resultados del modelo estadístico ajustado. Utilice el modelo para realizar predicciones sobre el futuro de la serie de tiempo.

9. Validación del modelo: Valide el modelo estadístico utilizando técnicas como la validación cruzada para asegurar generalización a nuevos datos. La validación permite evaluar la generalización del modelo a datos no utilizados en su ajuste.

10. Comunicación de resultados: Comunique los resultados del análisis de series de tiempo de manera clara y concisa. Utilice gráficos, tablas y resúmenes para presentar los hallazgos de manera efectiva.

Es importante tener en cuenta que este es un orden general recomendado. En algunos casos, puede ser necesario ajustar el orden u omitir algunas etapas, dependiendo de las características específicas de la serie de tiempo y de los objetivos del análisis.