Que es la robustez en estadística

La robustez en estadísticas se refiere a la capacidad de una medida estadística o método de análisis para funcionar bien o mantener su validez incluso en presencia de valores atípicos o datos inusuales. En el contexto de la estadística, una medida robusta es aquella que no se ve afectada significativamente por valores extremos en el conjunto de datos. La mediana es un ejemplo de una medida robusta, ya que tiende a mantener su valor central incluso cuando hay valores atípicos presentes.

Ejemplo de robustez en estadística

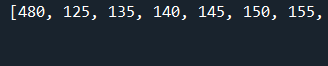
Imagina que tienes los clics mensuales en una página de un sitio web durante un año, representados por los valores: clicks_pagina_mes = [480, 125, 135, 140, 145, 150, 155, 160, 165, 155, 145, 450]. Para entender cómo evaluar nuestro rendimiento mensual, vamos a calcular la media y la mediana de estos datos. Después, haremos un gráfico para ver si hay valores atípicos que puedan afectar estas medidas. Finalmente, elegiremos la medida o parámetro más robusto y que nos ayude a entender cómo se comportan nuestros datos.

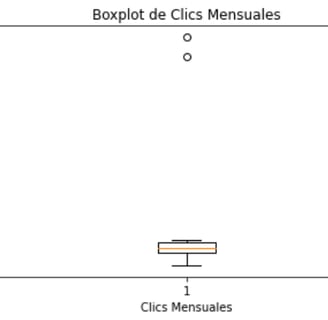
Como habíamos dicho la robustez estadística se refiere a la capacidad de las medidas centrales para resistir la influencia de valores atípicos en un conjunto de datos. Al comparar la media y la mediana, la robustez de la mediana se evidencia, ya que es menos afectada por valores extremos, proporcionando así una representación más fiable del centro de la distribución.

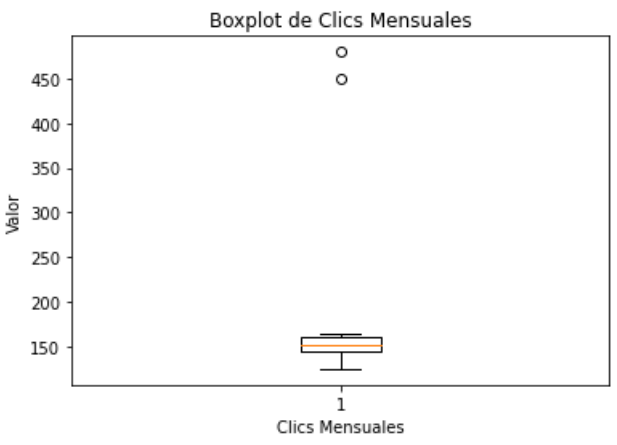
La identificación de valores atípicos se facilita mediante el análisis visual de un boxplot, donde los puntos fuera de los "bigotes" indican posibles valores atípicos, siendo útil para destacar cualquier desviación significativa en los datos. La presencia de valores atípicos, especialmente si son extremadamente grandes, puede sesgar considerablemente la media, mientras que la mediana se mantiene más robusta, siendo menos influenciada por estas anomalías.

En conclusión, descartaremos la media como parámetro para evaluar el rendimiento mensual de nuestra página web y optamos por la mediana como medida para nuestras evaluaciones de rendimiento mensual.