

Los momentos en estadística son medidas estadísticas que proporcionan información sobre la forma y la distribución de un conjunto de datos. Hay cuatro momentos principales: la tendencia central, la dispersión, la asimetría y la curtosis.
La Tendencia Central
Se mide a través Media, Mediana y Moda.
Media: También conocida como promedio, la media se calcula sumando todos los valores en un conjunto y dividiendo el resultado por el número total de observaciones. Es sensible a los valores extremos, ya que utiliza todos los datos en el cálculo. (ver como se calcula la media)
Mediana: La mediana es el valor que se encuentra en el centro de un conjunto de datos ordenado. Para calcularla, primero se ordenan los datos y luego se selecciona el valor que está en la posición central. La mediana no se ve afectada por los valores extremos y es especialmente útil cuando hay asimetría en la distribución. (ver como se calcula la mediana)
Moda: La moda es el valor que ocurre con mayor frecuencia en un conjunto de datos. A diferencia de la media y la mediana, la moda se centra en la frecuencia de los valores en lugar de sus magnitudes. Un conjunto de datos puede tener una moda (unimodal), más de una moda (multimodal) o no tener moda si todos los valores son diferentes. (ver como se calcula la moda)
La Dispersión o Variabilidad
Medidos por la Varianza, la Desviación Estándar y la Moda.
Varianza: La varianza mide la dispersión de los datos respecto a la media. Es la media de los cuadrados de las desviaciones de cada punto de datos con respecto a la media del conjunto. (ver como se calcula la varianza)
Desviación Estándar: La desviación estándar es simplemente la raíz cuadrada de la varianza. Proporciona una medida de dispersión en la misma unidad que los datos originales. (ver como se calcula la desviación estándar)
Rango: El rango es la diferencia entre el valor máximo y el valor mínimo en un conjunto de datos. Es una medida simple de la amplitud de los datos. (ver como se calcula el rango)
La Asimetría o Sesgo
La asimetría se refiere a la falta de simetría en la forma de la distribución de datos. En una distribución simétrica, los lados izquierdo y derecho son iguales o muy similares, mientras que en una distribución asimétrica, uno de los lados es más largo o ancho que el otro. Esto indica la tendencia de los datos hacia un extremo. Se mide a través del coeficiente de asimetría (CA).
Cómo se calcula la Asimetría
La asimetría se calcula a partir de coeficiente de asimetría (CA) se calcula utilizando la siguiente fórmula:
Donde:
n es el número de observaciones.
Xi es cada observación individual.
x̅ es la media de las observaciones.
S es la desviación estándar de las observaciones.
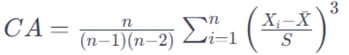
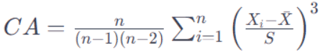
Tipos de la Asimetría
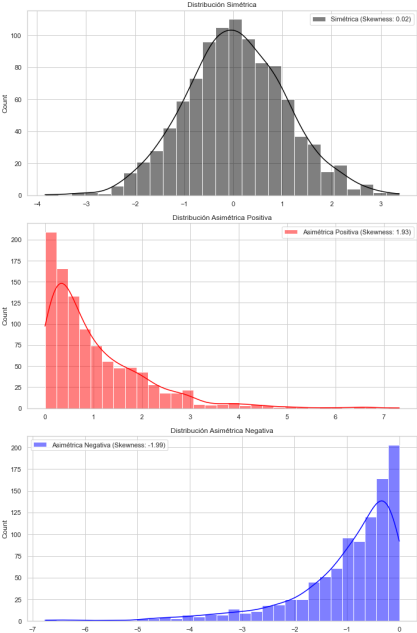
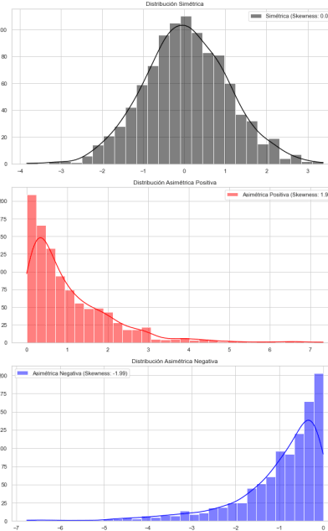
La Asimétrica 0 o Simetría (sin sesgo) es cuando obtenemos un coeficiente de asimetría igual a 0 (CA = 0). Esto implica que la distribución es simétrica, con ambos lados siendo iguales en forma y tamaño. La media, mediana y moda son todas iguales en una distribución simétrica.
Tenemos una Asimetría Positiva (sesgo a la derecha) cuando obtenemos un coeficiente de asimetría mayor a 0 (CA > 0). Esto significa que la cola derecha de la distribución es más larga o ancha que la izquierda. Es decir, la mayoría de los datos se concentran en el lado izquierdo, y hay valores extremos en el lado derecho.
Una Asimetría Negativa (sesgo a la izquierda) se evidencia cuando obtenemos un coeficiente de asimetría menor a 0 (CA < 0), lo cual indica que la cola izquierda de la distribución es más larga o ancha que la derecha y la mayoría de los datos se concentran en el lado derecho, y hay valores extremos en el lado izquierdo.
En resumen, el signo y el valor del coeficiente de asimetría proporcionan información sobre la dirección y la magnitud de la asimetría en una distribución de datos.
La Curtosis
La curtosis describe la forma de las colas de la distribución. Indica si las colas son más pesadas o más ligeras que las de una distribución normal. Una curtosis positiva sugiere colas más pesadas (más valores extremos), mientras que una curtosis negativa indica colas más ligeras y se mide mediante el coeficiente de curtosis (K).
Cómo se calcula la Curtosis
La fórmula para el coeficiente de curtosis (K) de una muestra de datos se expresa comúnmente como:
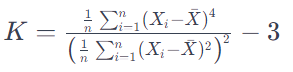
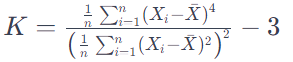
Donde:
n es el tamaño de la muestra.
Xi son los valores individuales en la muestra.
x̅ es la media de la muestra.
Tipos de Curtosis
La Mesocúrtica (Curtosis = 0), tiene un coeficiente de curtosis de 0 o muy cercana a 0, y su distribución es similar a una distribución normal estándar. La mayoría de las distribuciones normales caen en esta categoría.
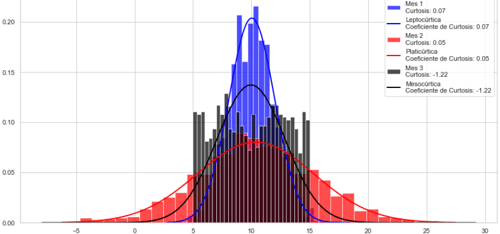
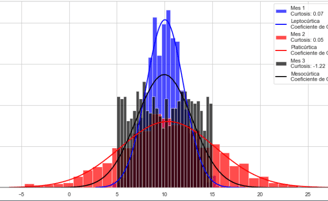
Por otro lado la Leptocúrtica (Curtosis > 0) tiene un coeficiente de curtosis mayor que 0. Las colas de la distribución son más pesadas y más pronunciadas en comparación con una distribución normal. Esto indica que la distribución tiene colas más altas y un pico más pronunciado en comparación con la distribución normal.
Finalmente la Platicúrtica (Curtosis < 0) tiene un coeficiente de curtosis menor que 0. Sus colas de distribución son más ligeras y más extendidas en comparación con una distribución normal. Esto indica que la distribución tiene colas más cortas y un pico más achatado en comparación con la distribución normal.
